归约待更新

注意

由于归约相关的 STLv2 设施尚不成熟：

rg::fold 在近期（2022 年 4 月）才被添加到 C++2b 标准中，无主流编译器支持；
rg::reduce 仍不在标准中

故只能使用传统版本 STLv1。待上述设施成熟后，本节需重写。

归约（Reduce）是另一种抽象的函数式操作，通常指将一系列数据变换到单独的一个数据。在日常生活中，求和就是一个归约操作：将一系列数据通过相加的方式得到一个单独的和。

\{1, 2, 3, 4, 5, 6\}\xrightarrow{\sum}21

折叠

简单的归约可以通过一种称为折叠（Fold）的模式来实现。首先需要一个初始值 $x_0$ 和一个（有意义的）二元函数 $f$ ，然后按照如下的流程计算折叠结果：

\bm a =\{x_1,x_2,\cdots,x_n\}\xrightarrow{\operatorname{fold_L}(f,x_0)}f\bigg(f\Big(f\big(f(x_0, x_1), x_2\big), x_3\Big)\cdots, x_n\bigg)\eqqcolon b

可能略微有些抽象。这里举一个例子，取初始值 $x_0=0$ ，二元函数 $f(a, b) = a + b$ 。此时，将 $\operatorname{fold_L}(f, x_0)$ 作用在范围 $\bm a=\{1, 2, 3, 4, 5, 6\}$ 的效果就是：

f(f(f(f(f(f(0, 1),2),3),4),5),6)=(((((0+1)+2)+3)+4)+5)+6=21\eqqcolon b

用图形的方式可以形象地描述为：

fold

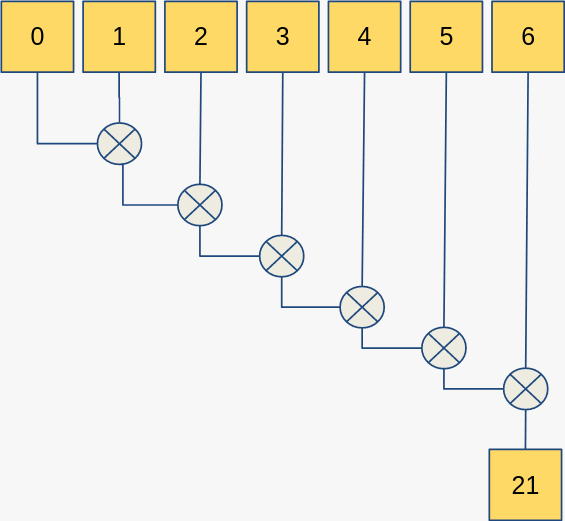
换句话说，折叠这种模式相当于用一个二元函数“遍历”整个范围。一般地，遍历的方向就是沿着迭代器自增的方向前进：首先用初始值 $x_0$ 和第一个元素 $x_1$ 做运算，然后再用运算结果和第二个元素 $x_2$ 做运算，直到结尾。这种折叠又称为左折叠（因此数学记号中我加上了 $L$ 下标）。反方向的还有右折叠；但一般不引起歧义时折叠就是指左折叠。

在 STLv1 中，std::accumulate 实现左折叠。下面的例子和之前一样，以 0 作为初始值，加法 std::plus{} 作为二元函数：

#include <iostream>
#include <vector>
#include <numeric> // 注意：这玩意儿不定义在 <algorithm>

int main() {
    std::vector a{1, 2, 3, 4, 5, 6};

    // 由于 STLv1 不支持范围概念，需要传入首尾迭代器
    // 初始值是 0，二元函数是 (a, b) -> a + b
    auto sum = std::accumulate(a.begin(), a.end(), 0, std::plus{});

    std::cout << sum << std::endl;
}

之所以命名为 std::accumulate，是因为二元函数参数带有默认实参，默认值就是 std::plus{}。此时，使用 std::accumulate 就是将一个范围内的元素求和，即累积（Accumulate）的含义。

类似地，如果将初始值设为 1，二元函数设为乘法 std::multiply{}，则效果就是求范围上所有元素的积。此外，如果传入的元素是 std::string 类型的，那么以 std::plus{} 函数 std::accumulate 整个范围就是在拼接字符串。你可以自己试一试，想一想原理。

并行归约

其实折叠只是一种特殊的归约。更通用的从二元函数导出的归约具有如下定义：

\{x_1,\cdots,x_n\}\xrightarrow{\operatorname{reduce}(f,\cdot)}\begin{cases} x_1,&n=1\\ f\big(\operatorname{reduce}(f,\{x_{i_1},\cdots,x_{i_k}\}),\operatorname{reduce}(f,\{x_{i_{k+1}},\cdots,x_{i_n}\})\big),&n>1 \end{cases}

其中 $\{i\}$ 是 $\{1,\cdots,n\}$ 的任意排列， $1\leqslant k\leqslant n$ 是任意正整数。

数学定义看上去总是令人脑袋大。简单来说，这是一个递归的定义：对于具有两个元素或更大的范围，则任意地拆成两半分别递归计算其归约结果。计算完成后，将两个结果用二元函数 f 运算，得到当前归约的结果。

它不同于折叠的最大区别在于“任意”二字。在对 $n$ 个元素的范围折叠时，总是先计算好前 $n - 1$ 个元素的折叠结果，然后再与 $x_n$ 运算。而这里则是任意划分运算顺序；它可以先将前 $k$ 个元素归约，然后再处理剩余的；甚至可以先对 $x_1,x_3,x_5,\cdots$ 归约，然后再对 $x_2,x_4,x_6\cdots$ 归约。具体如何运算取决于编译器和硬件如何处理。仍然是之前求和的例子，某次运算的过程可能如下图所示：

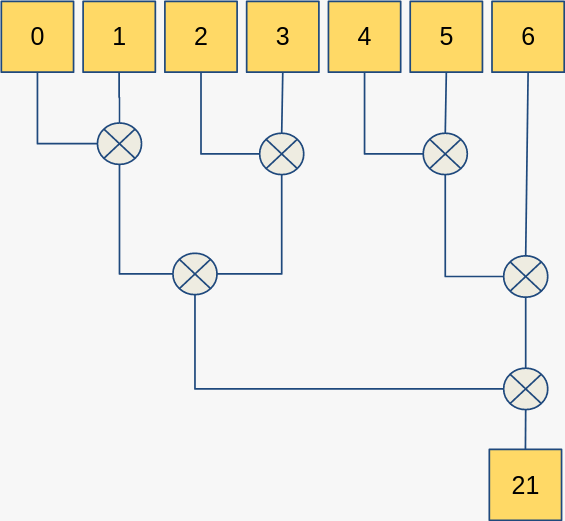
reduce

而到了不同的计算机、或者不同的编译器就会编译出不一样的运算顺序。这种任意性带来潜在的危险：只有当你的二元运算满足交换律和结合律时，才能保证结果是惟一的；否则，结果是不确值。但它也带来了好处：可以让计算机做并行优化。

并行优化是指，现代的计算机一般有两个以上的计算核心（核）。多个计算核心可以同时工作以加快整体运算速度；在之前的图示中，0 + 1 2 + 3 4 + 5 就可以同时计算。普通的折叠必须一步步挨排算，先算 0 + 1，然后 1 + 2，然后 3 + 3……总共需要花费六次计算时间，并行优化后则只用三次计算时间就可以完成。

STLv1 中，std::reduce 实现可并行优化的归约。使用上，前两个参数一般是首尾迭代器；第三个参数是初始值；第四个参数是二元函数。初始值是为了保证传入的范围不是空的（因为刚才的数学定义没有规定空范围的归约结果），默认实参是零值（具体而言，默认初始化的值）；二元函数同样默认为 std::plus{}。

std::accumulate 没有初始值的默认实参。

#include <iostream>
#include <vector>
#include <numeric> // 注意：这玩意儿也不定义在 <algorithm>

int main() {
    std::vector a{1, 2, 3, 4, 5, 6};

    // 初始值是 0，二元函数是 (a, b) -> a + b
    auto sum = std::reduce(a.begin(), a.end(), 0, std::plus{});
    // 或者使用默认实参
    std::reduce(a.begin(), a.end());

    std::cout << sum << std::endl;
}

此外，为了让编译器启用并行优化，还需要在参数列表中额外地传入一个提示 std::execution::par：

#include <iostream>
#include <vector>
#include <numeric> // 注意：这玩意儿也不定义在 <algorithm>
#include <execution>

int main() {
    std::vector a{1, 2, 3, 4, 5, 6};

    auto sum = std::reduce(std::execution::par, a.begin(), a.end());

    std::cout << sum << std::endl;
}

这个东西的学名叫“执行策略”（Execution policy），用来提示编译器做何种优化。比如 std::execution::seq 告诉编译器不要并行，只按顺序计算；而 std::execution::unseq 提示编译器使用 SIMD 等类似向量化手段优化。

# 归约 待更新

# 折叠

# 并行归约

归约待更新

折叠

并行归约