二维数组
既然数组也是一种变量类型,那么是否存在数组的数组呢?答案是肯定的。
假设我们有三个 int[4] 类型的数组。然后这三个数组又构成了一个“大”的数组,它就声明为:
int a[3][4]{};
这个 a 就是数组的数组。它拥有三个元素 a[0] a[1] a[2],这三个元素的类型都是 int[4] 类型。因此每个元素又包含四个元素;比如 a[0] 又拥有四个元素 a[0][0] a[0][1] a[0][2] a[0][3]。如果用图表示出来的话,就长成这样: 
图中,整个 int[3][4] 类型的 a 分为 3 个“行”,每一“行”就是一个 int[4] 类型的 a 的元素。而每一个 int[4] 又包含 4 个 int 类型的元素(也就是 4 个“列”)。所以如果形象地理解,一位数组像是“一条线段”,二维数组就像是“一个长方形”。
二维数组的初始化
首先是最容易理解的初始化方法:
int a[3][4]{
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
经过这样的初始化后,a[0] 被初始化为 {1, 2, 3, 4},a[1] 被初始化为 {5, 6, 7, 8},a[2] 被初始化为 {9, 10, 11, 12}。也就是如下图所示: 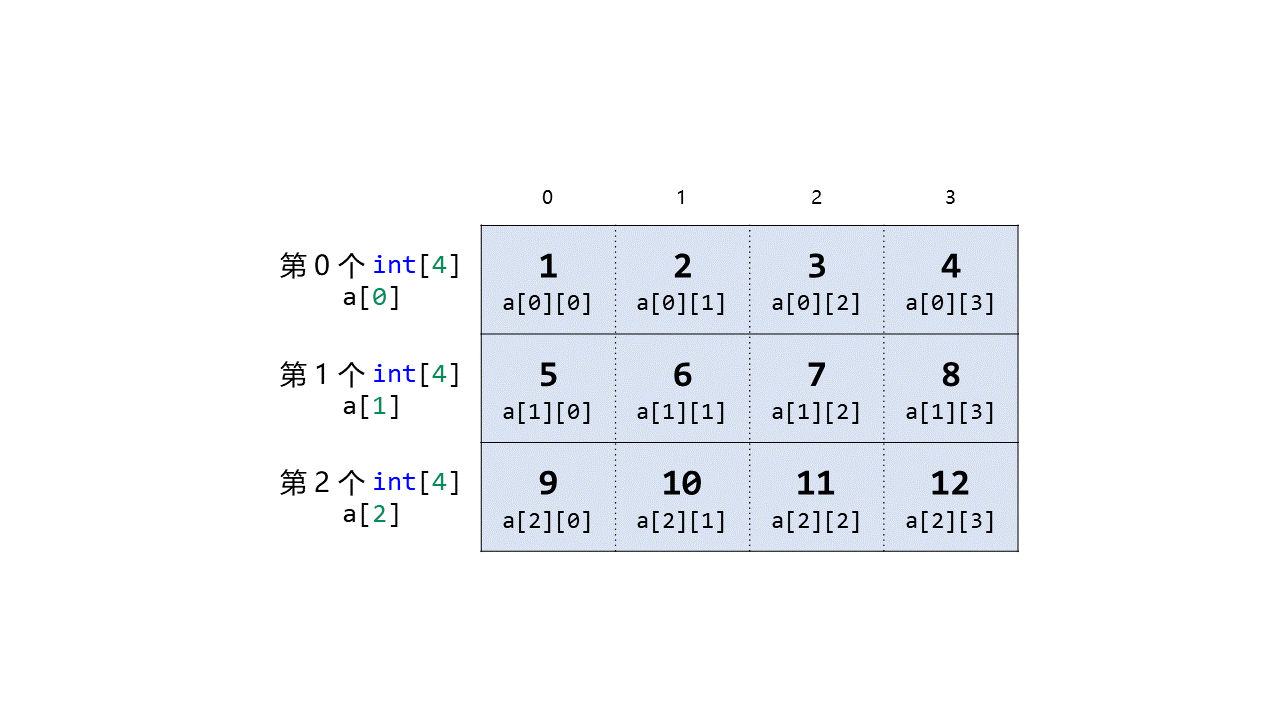
这种写法和一维数组的初始化没有太多差别,只是将“大括号列表”进行了两层的嵌套而已。所以一位数组的其它初始化方法也大多适用。比如下面的代码提供较少的初始化值,没有提供初始化值的元素仍然被初始化为 0。
它的运行结果是:
1 0 0 0
2 3 0 0
4 5 6 0
你还可以这样初始化:不给 a[2] 这个数组提供初始化器,也就是只初始化了 a[0] 和 a[1]。
这样当然没问题,效果就是零初始化 a[2],第三行 a[2] 中的每个元素都为 0:
1 2 3 4
5 6 7 8
0 0 0 0
正因如此,我们可以省略所有初始化值,写成这个样子。
此时,a 中的 3 个 int[4] 全部采用零初始化——也就意味着,12 个 int 的值全部初始化为 0。
这种逐元素初始化的方法称为聚合初始化(Aggregate initialization)。可以被聚合初始化的类型是聚合类型(Aggregate type)。所有数组类型都是聚合类型。聚合初始化时,有时可以省略内部嵌套的大括号,如
int a[2][2]{{1, 2}, {3, 4}};可省作int a[2][2]{1, 2, 3, 4};。
三维数组及更多维
二维数组也是变量;所以如果构造一个由二维数组构成的数组,就形成了一个三维数组。比如:
int b[5][3][4]{};
数组 b 是有 5 个 int[3][4] 类型的元素构成,如下所示: 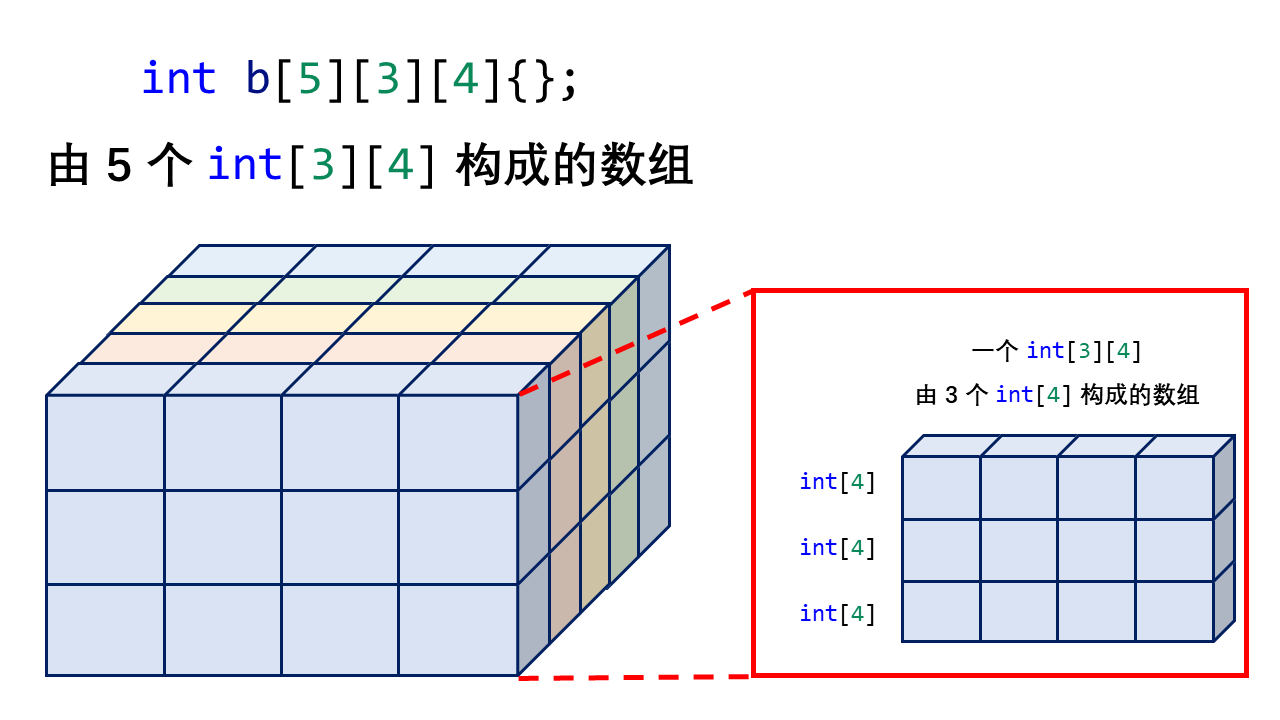
同样地,由三维数组构成的数组称为四维数组……你可以这样一直做下去,道理是一样的,我们便不再详细说明了。