递归

从普通调用说起

首先从一个简单的例子入手。编写这样一个程序：输入一个大于 1 的整数，判断它是否为质数。那么根据质数的定义，你可以写出这样的代码。

#include <iostream>
using namespace std;
bool isPrime(int x) {
    for (int i{2}; i < x; i++) {
        if (x % i == 0)   // 只要存在一个能除尽的约数
            return false; // 就不是质数
    }
    return true;          // 所有比它小的都除不尽，就是质数
}
int main() {
    int a;
    cin >> a;
    if (isPrime(a))
        cout << "Prime" << endl;
    else
        cout << "Not prime" << endl;
}

然后你会注意到在函数 isPrime 中，如果形参 x 有约数，那么必有一个小于等于它平方根的约数。因此我们可以充分利用定义在头文件 <cmath> 里的 std::sqrt 函数计算平方根。

#include <iostream>
#include <cmath>         // 这里增加一个头文件引入
using namespace std;
bool isPrime(int x) {
    int r;
    r = sqrt(x);                  // 计算平方根
    for (int i{2}; i <= r; i++) { // r 为上界
        if (x % i == 0)   // 只要存在一个能除尽的约数
            return false; // 就不是质数
    }
    return true;          // 所有比它小的都除不尽，就是质数
}

#include <iostream>
#include <cmath>         // 这里增加一个头文件引入
using namespace std;
bool isPrime(int x) {
    int r;
    r = sqrt(x);                  // 计算平方根
    for (int i{2}; i <= r; i++) { // r 为上界
        if (x % i == 0)   // 只要存在一个能除尽的约数
            return false; // 就不是质数
    }
    return true;          // 所有比它小的都除不尽，就是质数
}
int main() {
    int a;
    cin >> a;
    if (isPrime(a))
        cout << "Prime" << endl;
    else
        cout << "Not prime" << endl;
}

一般地，sqrt 函数的声明为 double sqrt(double arg);。因此在上述代码第六行调用过程中，发生了整型与浮点类型之间的隐式转换。（这里忽略了许多细节，实际上 sqrt 接收整型实参时可能是一个模板函数。）

这样速度会快不少。如果你把整个程序的结构用之前的图示标示出来的话，就长成这样：

所以函数可以像这样一层一层嵌套起来调用。那么问题就来了，一个函数能否“调用它自己”？

认识递归

这个“调用自己”听上去特别玄乎。还是用一个例子来引入好了：求一个正整数的阶乘 $n! =\displaystyle \prod_{i=1}^ni=1\times2\times\cdots\times n$ 。你能否不适用循环语句来实现吗？

可以这样考虑，将 $n!$ 定义为：

1! = 1

n! =(n-1)!\times n

这样就可以

\begin{aligned} 2!&= 1!\times 2=&2\\ 3!&= 2!\times 3=&6\\ 4!&= 3!\times 4=&24\\ &\qquad\cdots& \end{aligned}

如此一路推算下去。如果用函数 int fact(int); 来表示阶乘的话，则 fact(n) 的值与 n * fact(n - 1) 的值相等。可以把这一思想这样表示出来：

#include <iostream>
using namespace std;
int fact(int n) {
    if (n == 1) {
        return 1;
    } else {
        return n * fact(n - 1);
    }
}
int main() {
    cout << fact(4) << endl;
}

理解起来有难度？其实不用想太多，这种写法和原来的普通调用没有任何区别。请看下面的图示：

我们称这种在函数体内调用函数自身的编程方法为递归（Recursion）。从刚才的图中也可看出，递归式的调用与普通的函数嵌套调用是一样的，都是“一层一层”地执行，然后从内到外“一层一层”地返回到调用方。

递归唯一比较特殊的地方在于它需要有一个递归终止的条件。试想如果刚才的 fact 函数中缺少 if (n == 1) return 1; 这个判断的话，则调用将持续不断、永不停止地进行下去——直到计算机的内存放不下那么多函数的空间为止（这种现象俗称“爆栈”）。所以在进行递归调用前需要谨慎地考虑它终止的条件。

经典例题

说到递归，跑不了的就是这个著名的“汉诺塔问题”：

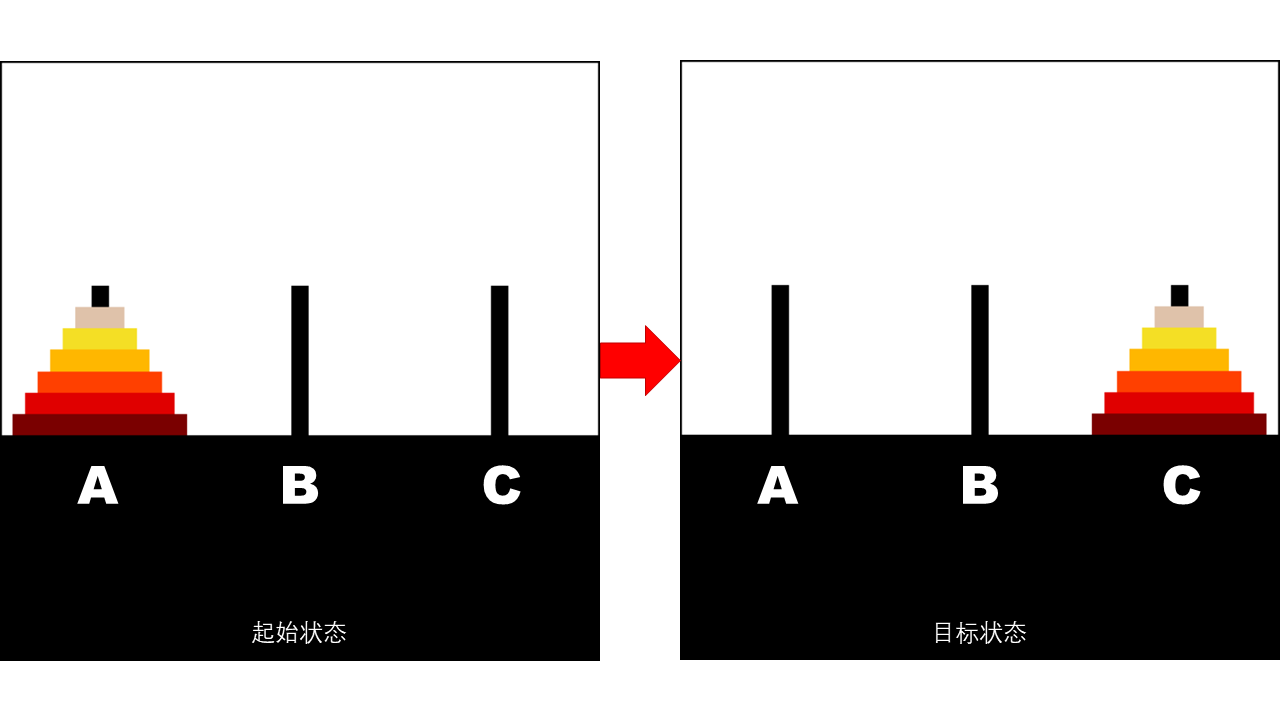
相传在古印度圣庙中，有一种被称为汉诺塔的游戏。该游戏是在一块铜板装置上，有三根杆（编号 A、B、C），在 A 杆自下而上、由大到小按顺序放置 $n$ 个金盘。游戏的目标：把 A 杆上的金盘全部移到 C 杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下、小盘在上，操作过程中盘子可以置于 A、B、C 任一杆上。下面的图示为 $n=6$ 的情形：

Hanoi

提示

汉诺塔问题经常用作递归的入门例题，但是它理解起来的难度仍然比较大。不过我敢确定的是，如果你能理解这道题，那么你就掌握了递归的核心要点。这也是为什么这里会选它作为例题。我会尽量清楚地去解释这个过程，但是也不能够保证完全讲明白。如果你看了很久还是没有理解的话，姑且跳过去吧，等有了更多的编程经验之后再回过头来看也不晚。

我们想编写一个程序来做这件事情。输入一个整数 n，输出移动盘子的步骤。为了解决这个问题，我现在先写一个函数：

void moveDisk(int n, char src, char dest, char trans);

这个函数是做什么的呢？当执行它的时候，它会输出将 n 个（前 n 小的）盘子从 src 这根杆挪到 dest 这根杆的步骤。其中 src 就是起始杆， dest 就是目标杆。最后剩下的那根杆被称为“中转杆”。比如我们的目标就是将 n 个盘子从杆 A 移动到杆 C，那么直接执行 moveDisk(n, 'A', 'C', 'B'); 就可以输出中间的步骤了。为了行文方便，称最小的盘子为 1 号盘，比它大一点的称为 2 号盘……最大的那个盘子称为 n 号盘。那么怎么去实现这个 moveDisk 函数呢？

先考虑最简单的情况：n 为 1 的时候。如果只有一个盘子，那么直接将它从起始杆挪到目标杆就可以了。也就是：

void moveDisk(int n, char src, char dest, char trans) {
    if (n == 1) {
        // 将 1 号盘（最小的）从 src 杆挪到 dest 杆
        cout << "Move disk 1 from " << src << " to " << dest << endl;
        return;
    }
    // [...]
}

现在考虑 n 为 2 的情形。我们想要把两个盘子从 A 杆挪到 C 杆。怎么做呢？稍微尝试以下就可以得出这样的解法：

将最小的 1 号盘从 A 杆挪到 B 杆；
将 2 号盘从 A 杆挪到 C 杆；
将 1 号盘从 B 杆挪到 C 杆。

这两种情况是比较简单的。现在来看 n 为 3 的情形：要把三个盘子从 A 杆挪到 C 杆。同样也分为 3 步：

将 1 号、2 号两个盘子从 A 杆挪到 B 杆；
将 3 号盘从 A 杆挪到 C 杆；
将 1 号、2 号两个盘子从 B 杆挪到 C 杆。

这里，第二步没有问题。第一步和第三步如何同时移动两个盘子呢？没关系，只要稍微考虑一下就可以：

将 1 号、2 号两个盘子从 A 杆挪到 B 杆，具体做法是：
1. 将 1 号盘从 A 杆挪到 C 杆；
2. 将 2 号盘从 A 杆挪到 B 杆；
3. 将 1 号盘从 C 杆挪到 B 杆；
将 3 号盘从 A 杆挪到 C 杆；
将 1 号、2 号两个盘子从 B 杆挪到 C 杆。
1. 将 1 号盘从 B 杆挪到 A 杆；
2. 将 2 号盘从 B 杆挪到 C 杆；
3. 将 1 号盘从 A 杆挪到 C 杆；

稍微停顿一下。这里你会发现两个拆开的步骤非常相似。它们和之前挪两个盘子的步骤是一致的，都是：

1 号：起始杆 → 中转杆
2 号：起始杆 → 目标杆
1 号：中转杆 → 目标杆

事实上，将 3 个盘子整个从 A 杆挪到 C 杆也是这样的过程！

1,2 号：起始杆 → 中转杆
3 号：起始杆 → 目标杆
1,2 号：中转杆 → 目标杆

所以就发现了规律。如果你要将 n 号盘子从 src 杆挪走，你首先需要把上面碍事的 n - 1 个盘子放到一边去（放在 trans 杆上）。等把这 n - 1 个盘子处理妥当了，就可以安安稳稳地将 n 号盘子挪到 dest 杆。最后，只需要再把刚才撂在一边的 n - 1 个盘子放回 dest 杆上就行了。这个过程就是这样的：

// 将上面 n - 1 个盘子放在中转杆上
moveDisk(n - 1, src, trans, dest);
// 将 n 号盘子放在目标杆上
cout << "Move disk " << n << " from " << src << " to " << dest << endl;
// 将 n - 1 个盘子放到目标杆上
moveDisk(n - 1, trans, dest, src);

所以整段代码就是这样的：

#include <iostream>
using namespace std;
void moveDisk(int n, char src, char dest, char trans) {
    if (n == 1) {
        cout << "Move disk 1 from " << src << " to " << dest << endl;
        return;
    } // 因为这里 return 了，所以不需要写 else
    moveDisk(n - 1, src, trans, dest);
    cout << "Move disk " << n << " from " << src << " to " << dest << endl;
    moveDisk(n - 1, trans, dest, src);
}
int main() {
    int n;
    cin >> n;
    moveDisk(n, 'A', 'C', 'B');
}

下面这张图片展示了这个递归的思想。每一个步骤都分为三个小部分，直到最简单的情形（点击可展开/收起下一层过程）：

有人说，递归思想就是将一个大规模的问题转移到较小规模的同类问题。所以在解决递归问题时，只需考虑问题的转移方法和终止条件就够了。

可参考更形象的描述：如何理解汉诺塔的递归？ - Fireman A的回答 - 知乎open in new window

递归是一个非常重要的概念，它在各个领域都有诸多的用途。不过由于本书的侧重点不在算法，所以不会再展开讲。有一种极为有用的算法被称为“深度优先搜索”（DFS），它的核心就是递归思想；感兴趣的读者可以查阅相关资料，这里不再赘述。

# 递归

# 从普通调用说起

# 认识递归

# 经典例题

# 更多

递归

从普通调用说起

认识递归

经典例题

更多