初识函数

从数学谈起

数学上的函数读者应当都有所了解。我们先陈述一下数学上函数的定义：设有两个数的集合 $A$ 和 $B$ ，并存在一种对应关系 $f$ 使得对于集合 $A$ 中任意一个元素 $a$ ，在集合 $B$ 中都存在唯一的一个元素 $b$ 与之对应，则记作：

\begin{aligned} f:&A\to B\\ &a\mapsto b \end{aligned}

，也记作 $b=f(a)$ 。称集合 $A$ 为定义域，称集合 $B$ 为陪域。数学上，称 $a$ 是函数 $f$ 的变元；物理上，称 $a$ 为自变量，称 $b$ 为因变量。

陪域和值域 $f(A)$ 是不同的，但这是数学上的概念辨析，这里不做展开。

比如函数 $y=\sin(x)$ 中， $\sin$ 是对应法则，而 $y$ 是因变量， $x$ 是自变量。同时，我们默许了定义域和陪域都是实数域 $\mathbb R$ 。（值域是区间 $[-1,1]$ 。）

计算机中的“函数”

数学上的函数可以在计算机中表现出来。比如现在考虑一个非常简单的一次函数： $f(x)=2x+1$ ，其中定义域为全体整数 $\mathbb Z$ ，陪域也是全体整数 $\mathbb Z$ 。我现在想在 C++ 程序上把这个函数“表现”出来——但是显然计算机表达不了全体整数（因为整数有无穷多个，但计算机的存储空间是有限的），所以咱们暂时就把定义域和陪域都限制在 int 类型的表达范围内。那么写成这个样子就可以定义函数 $f(x)$ ：

int f(int x) {
    return 2 * x + 1;
}

读者们看了可能一脸懵逼，这啥玩意儿啊？请看下图，这段代码里面至少体现了一个函数的几个关键信息：定义域、陪域、函数名以及函数的解析式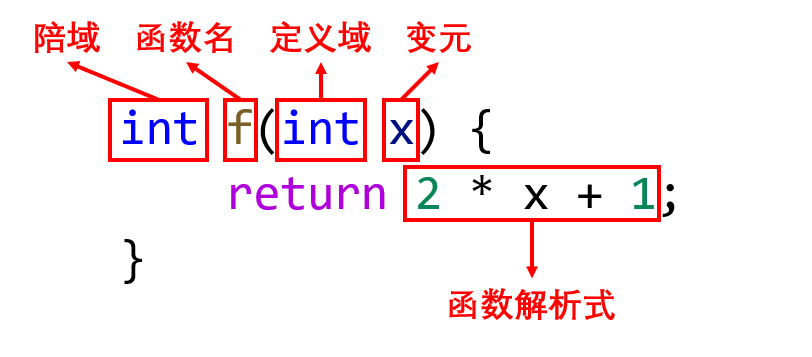： function

目前咱们先不要管“为什么写成这个鬼样子”、“return 是啥意思”，照葫芦画瓢写就是了。

你可以把这段代码放在 int main() { 的上面，然后你就可以像数学上的写法一样去使用这个函数。请看下面的例子：

#include <iostream>
using namespace std;
int f(int x) {
    return 2 * x + 1;
}
int main() {
    int x{42};
    int y{0};
    y = f(x); // 使用刚才的函数 f(x)
    cout << y << endl;
}

这里 3 ~ 5 行定义了刚刚的那个函数 $f$ ，然后第九行使用了这个函数——令变量 y 的值为 f(x)。其中 x 的值为 42，因此 f(x) 的值为 85。因此 y 赋值后就得到了 85：

为了演示，我再举一个二次函数的例子： $g(x)=x^2-4x+1$ 。那么我可以这样在 C++ 中表示它：

int g(int x) {
    return x * x - 4 * x + 1;
}

同样地，你可以像刚才那样去使用这个函数。把这段代码放在最上面：

#include <iostream>
using namespace std;
int g(int x) {
    return x * x - 4 * x + 1;
}
int main() {
    int x, y;
    cin >> x;
    y = g(x); // 使用刚才的函数 g(x)
    cout << y << endl;
}

编译运行的效果是：

¶-5↵
46

现在来考虑绝对值函数 $\operatorname{abs}(x)=|x|$ 。该如何在 C++ 中表示这个函数呢？根据定义：

\operatorname{abs}(x)=\begin{cases} x,&x\geqslant0\\ -x,&x<0 \end{cases}

那么我可以用条件表达式来写出它的解析式：

unsigned int abs(int x) {  // 陪域设置为 unsigned int，因为绝对值必然是非负的
    return x >= 0 ? x : -x;
}

看上去不错；你也可以像刚才那样试着去使用它。最后来看一看符号函数 $\operatorname{sgn} x$ 。它数学上的定义是：

\operatorname{sgn}x=\begin{cases} 1,&x>0\\ 0,&x=0\\ -1,&x<0 \end{cases}

那么同样运用条件表达式——

int sgn(int x) {
    return x > 0 ? 1 : x == 0 ? 0 : -1;
}

停停停。你会发现这样写有点太乱了，对吧。那么其实我们可以把条件表达式改成 if 语句的形式……

int sgn(int x) {
    int y;
    if (x > 0) {
        y = 1;
    } else if (x == 0) {
        y = 0;
    } else {
        y = -1;
    }
    return y;
}

就像我们原来写代码那样。先设置一个变量 y 用于存放整个函数计算出来的值，随后根据不同的 x 判断 y 应该赋什么值。这时，变量 y 的值就代表了 sgn(x) 这个函数应该是多少（相当于原来解析式的作用），因此只要把 y 放在 return 后面就好。

上面的代码中，我们在第 2 行到第 9 行以 C++ 语言的形式实现了函数的对应法则。

多元函数

数学上有一种函数叫多元函数。多元函数是指将有序数组 $(x_1,x_2,\cdots,x_n)$ 通过某个对应规则 $f$ 映射到唯一对应的数 $y$ 上，记作

y=f(x_1,x_2,\cdots,x_n)

多元函数的准确定义需要用到笛卡尔积的概念，然而这里为了避免晦涩难懂的词汇从而不展开讲解。

最常见的多元函数就是最大值函数 $\max$ 了。比如 $\max\{x_1,x_2,\cdots,x_n\}$ 就是取 $x_1,x_2,\cdots,x_n$ 这些变元中最大的那个。

同样地，C++ 中可以很方便地将多元函数表达出来。用接受两个变元的最大值函数 $\max\{x_1,x_2\}$ 举例，我们可以轻松地写出解析式

\max\{x_1,x_2\}=\begin{cases} x_1,&x_1>x_2\\ x_2,&x_1\leqslant x_2 \end{cases}

那么把它用刚刚学过的那个葫芦装起来：

int max(int x1, int x2) {
    return x1 > x2 ? x1 : x2;
}

当然你也可以用语句来代替条件表达式：

int max(int x1, int x2) {
    int y;
    if (x1 > x2) {
        y = x1;
    } else {
        y = x2;
    }
    return y;
}

然后你就可以这样去使用这个多元函数：

#include <iostream>
using namespace std;
int max(int x1, int x2) {
    return x1 > x2 ? x1 : x2;
}
int main() {
    int a, b;
    cin >> a >> b;
    cout << max(a, b) << endl;
}

这段程序会输出输入的两个数之中较大的那个。

不管怎么说，目前你知道 C++ 有一种神奇的写法可以表达出一个数学上简单的函数或者多元函数。当这个函数表达出来之后，你可以用一种很直接的方式（比如 y = f(x)）去使用它。那么这就是你对 C++ 中函数的初步认识。

直到现在我们仍然没有给出 C++ 中函数的具体定义。下一节中我们将进行更详细的学习。

# 初识函数

# 从数学谈起

# 计算机中的“函数”

# 多元函数

初识函数

从数学谈起

计算机中的“函数”

多元函数